Rechengesetze in Klasse 3: Rechnen mit Regeln wird leichter

Manchmal sehen Rechenaufgaben aus wie ein kleiner Knoten im Kopf: viele Zahlen, ein paar Zeichen und vielleicht noch Klammern. Die gute Nachricht: Es gibt Rechengesetze. Das sind Regeln, die immer stimmen. Sie helfen Kindern, Aufgaben übersichtlich zu machen und schneller zu prüfen, ob ein Ergebnis logisch ist.
Für Eltern ist das beruhigend: Ihr Kind muss nicht „Tricks“ auswendig lernen. Es lernt, warum etwas klappt. Und genau das macht Mathe in der 3. Klasse stabil und sicher.
Was sind Rechengesetze – und warum sind sie wichtig?

Rechengesetze sind feste Regeln, wie man mit Zahlen rechnen darf. Sie sind wie Verkehrsregeln: Wenn alle sie kennen, wird es sicher und einfacher.
- Sie machen Aufgaben leichter. Man darf umsortieren oder zusammenfassen.
- Sie helfen beim Kontrollieren. Man kann auf einem zweiten Weg prüfen.
- Sie passen zum Alltag. Dinge zählen, Gruppen bilden, Preise zusammenrechnen.
Ein Beispiel: Du hast 3 rote und 5 blaue Bonbons. Ob du erst die roten zählst oder erst die blauen: Am Ende sind es 8. Diese Idee steckt in einem Rechengesetz.
Mathematische Teile erkennen: Zahl, Rechenzeichen, Klammern
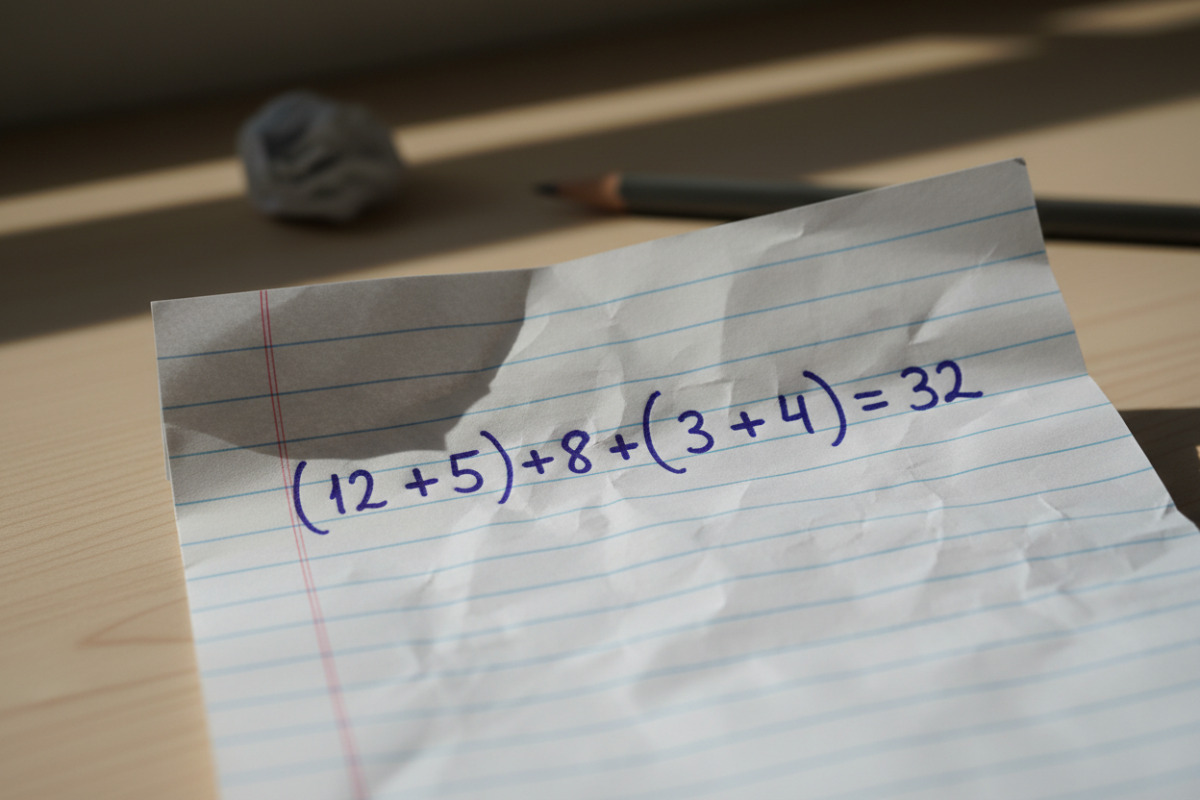
Bevor man Regeln nutzt, hilft es, eine Rechnung wie ein Bauwerk zu sehen. Jede Rechnung besteht aus Teilen:
- Zahlen (z. B. 4, 12, 30)
- Rechenzeichen: Plus +, Minus −, Mal ·, Geteilt :
- Klammern ( ): Sie zeigen, was zusammengehört.
Eine gute Übung für Kinder: Eine Aufgabe wie (8 + 2) + 5 mit dem Finger abfahren und laut sagen: „Klammer auf, acht plus zwei, Klammer zu, plus fünf.“
Wenn ihr solche Bausteine trainieren möchtet, hilft auch die Übungseite Teile der Rechnung erkennen.
Addition mit Klammern: Reihenfolge verstehen

Klammern sind wie eine kleine „Jetzt zuerst!“-Ansage. In der 3. Klasse ist die wichtigste Regel:
Zuerst rechnest du, was in der Klammer steht. Danach rechnest du mit dem Ergebnis weiter.
Beispiel mit Bauklötzen: In einer Kiste liegen 6 blaue und 4 gelbe Klötze. Später kommen noch 3 rote dazu.
- Rechnung: (6 + 4) + 3
- Erst in der Klammer: 6 + 4 = 10
- Dann weiter: 10 + 3 = 13
Wichtig für Eltern: Viele Kinder wollen „einfach von links nach rechts“ rechnen. Das klappt oft, aber bei Klammern ist das Rechengesetz eindeutig. Darum lohnt sich das ruhige Lesen der Aufgabe.
Verknüpfungs- und Vertauschungsgesetz der Addition (mit Beispielen)

Bei der Addition gibt es zwei besonders praktische Rechengesetze. Die Namen klingen groß, aber die Idee ist einfach.
1) Vertauschungsgesetz: Die Reihenfolge ist egal
Wenn du Zahlen addierst, darfst du sie vertauschen. Das Ergebnis bleibt gleich.
- 4 + 7 = 7 + 4
- Alltag: Erst 2 Äpfel in den Korb, dann 5 – oder andersrum. Es sind trotzdem 7.
2) Verknüpfungsgesetz: Du darfst anders klammern
Bei drei (oder mehr) Plus-Zahlen darfst du entscheiden, welche du zuerst zusammenrechnest.
- (3 + 5) + 2 = 3 + (5 + 2)
Das ist hilfreich, wenn du „schöne“ Paare findest:
- Beispiel: 8 + 2 + 5
- Schön ist: 8 + 2 = 10
- Also: (8 + 2) + 5 = 10 + 5 = 15
Gleichmachen von Aufgaben mit Klammern
„Gleichmachen“ bedeutet: Wir verändern das Aussehen der Aufgabe, aber nicht den Wert. Das ist wie beim Umräumen von Bauklötzen: Der Turm sieht anders aus, aber es sind gleich viele Klötze.
Beispiele (Addition):
- 6 + 4 + 3 kann man zu (6 + 4) + 3 machen.
- Oder zu 6 + (4 + 3).
Wann ist das besonders nützlich?
- Wenn Ihr Kind schnell einen Zehner bilden will: 7 + 3 + 9 → (7 + 3) + 9 = 10 + 9
- Wenn das Kopfrechnen leichter werden soll.
Wichtig: Dieses „Gleichmachen“ klappt bei Plus sehr gut. Bei Minus muss man vorsichtiger sein. Darum üben Kinder in Klasse 3 vor allem: Plus darf oft umgestellt und umklammert werden.





Fünf Alltagsszenen zeigen, wie Kinder Mengen ordnen, Klammern lesen und Aufgaben prüfen.
Eigenschaften der Multiplikation: Mal-Aufgaben clever verstehen
Multiplikation bedeutet: gleich große Gruppen. Statt „3 + 3 + 3 + 3“ kann man „4 · 3“ schreiben.
Auch bei Mal gibt es Regeln:
- Vertauschen geht: 3 · 5 = 5 · 3. (3 Reihen mit 5 Punkten sind genauso viele wie 5 Reihen mit 3 Punkten.)
- Zusammenfassen geht: (2 · 3) · 4 = 2 · (3 · 4). Die Reihenfolge der „Päckchen“ ist egal.
- Mit 1: 1 · 7 = 7 (eine Gruppe mit 7 bleibt 7).
- Mit 0: 0 · 7 = 0 (null Gruppen ergeben null).
Wenn Sie dazu passende Übungen suchen, finden Sie bei Schlaumik weitere Beispiele zu Eigenschaften der Multiplikation.
Multiplikationsaufgaben vergleichen: Was ist größer, was ist gleich?
Kinder vergleichen oft Aufgaben wie: „Ist 3 · 6 größer als 2 · 9?“ Das klappt gut, wenn man sich Gruppen vorstellt.
- 3 · 6: 3 Gruppen mit je 6 Murmeln → 18
- 2 · 9: 2 Gruppen mit je 9 Murmeln → 18
Sie sind also gleich groß, obwohl die Aufgabe anders aussieht. Hier merken Kinder: Rechengesetze helfen beim Vergleichen, ohne alles neu zu zählen.
Praktischer Eltern-Tipp: Lassen Sie Ihr Kind kleine Punktbilder malen (z. B. 3 Reihen mit 6 Punkten). Dann sieht man Gleichheiten oft sofort.
Wann sind zwei Rechenausdrücke gleich?
Zwei Rechenausdrücke sind gleich, wenn sie am Ende denselben Wert haben. Das gilt auch, wenn sie ganz unterschiedlich aussehen.
Beispiele:
- 7 + 5 ist gleich 10 + 2 (beides 12).
- 4 · 6 ist gleich 2 · 12 (beides 24).
Ein guter Prüf-Weg für Kinder: „Kann ich es mir als Gruppen vorstellen?“ Wenn beide Bilder gleich viele Dinge zeigen, sind die Ausdrücke gleich.
Auf Schlaumik gibt es dazu passende Aufgaben zum Thema Gleichheit von Ausdrücken.
Das Distributivgesetz: Mal verteilt sich auf Plus
Das Distributivgesetz klingt kompliziert, ist aber eine sehr alltagstaugliche Idee: Wenn du mehrere gleiche Gruppen hast, kannst du sie aufteilen.
Beispiel mit Bonbons:
- Du hast 4 Tüten.
- In jeder Tüte sind 3 rote und 2 gelbe Bonbons.
- Also: 4 · (3 + 2)
Jetzt gibt es zwei gleich richtige Wege:
- Erst in der Klammer: (3 + 2) = 5, dann 4 · 5 = 20
- Oder verteilen: 4 · 3 + 4 · 2 = 12 + 8 = 20
Merksatz für Kinder: „Mal kann man auf Plus verteilen.“
Wenn Ihr Kind diese Idee üben möchte, passt die Seite Distributivgesetz üben sehr gut.
Zusammenhang zwischen Addition und Multiplikation
Multiplikation ist eine Abkürzung für wiederholtes Addieren.
- 5 · 3 bedeutet: 3 + 3 + 3 + 3 + 3
- 2 · 8 bedeutet: 8 + 8
Alltag: 6 Tage lang bekommst du jeden Tag 2 Sticker. Dann hast du 6 · 2 = 12 Sticker. Du könntest auch 2 + 2 + 2 + 2 + 2 + 2 rechnen. Mal ist nur schneller.
Für Eltern ist das wichtig, wenn ein Kind Mal-Aufgaben noch nicht „auswendig“ kann: Es darf erst addieren. Mit der Zeit wird es automatisch schneller.
Zusammenhang zwischen Multiplikation und Division
Division ist das „Rückwärtsdenken“ zur Multiplikation.
- Wenn 4 · 5 = 20, dann gilt auch 20 : 5 = 4 und 20 : 4 = 5.
Beispiel: Du hast 20 Kekse und willst sie auf 5 Kinder verteilen. Wenn jedes Kind gleich viele bekommt, ist das eine Division: 20 : 5. Wer die Mal-Aufgabe kennt, findet die Division leichter.
Mein Kind vertauscht bei Klammern manchmal die Reihenfolge – was hilft?
Hilfreich ist ein fester Ablauf: 1) Aufgabe laut lesen, 2) Klammerteil mit dem Finger einkreisen, 3) erst die Klammer rechnen, 4) Ergebnis in die Aufgabe „einsetzen“ und weiterrechnen. Arbeiten Sie mit kleinen Geschichten: „In der Klammer packen wir zuerst die Tüte.“ Und: lieber wenige Aufgaben ganz sauber rechnen als viele schnell. So wird die Reihenfolge zur Gewohnheit.
Mini-Checkliste: So übt ihr Rechengesetze im Alltag
- Beim Einkaufen: „Wenn wir erst 2 Euro und dann 3 Euro dazunehmen – ist das andersherum gleich?“
- Beim Aufräumen: Bauklötze in Gruppen legen: „3 Gruppen à 4 Klötze“.
- Beim Teilen: Kekse fair verteilen: „20 Kekse auf 4 Teller“.
- Beim Kopfrechnen: Zehnerfreunde suchen und passend klammern: (8+2)+7.
Wenn Kinder merken, dass Regeln echte Hilfe sind, entsteht etwas Wichtiges: Mathe fühlt sich nicht mehr wie Raten an, sondern wie logisches Denken.







